Paryavarta Yojayet is another important Vedic Maths Sutra that we are going to learn. Paryavarta Yojayet translates to Transpose and Apply. Transpose means to change the sign of a given number i.e Subtraction becomes Addition and Vice- versa. These numbers are then applied to the process. It is used to divide numbers where the divisor is slightly greater than any power of 10 and starts with 1. The Vinculum process that we learned earlier will also be applied numerous times while we apply this method of division.
Vinculum numbers are those numbers that have 1 negative digit or have a Bar over them (indicating that it is a negative digit).
Through the Place Value System in Vedic Math normal numbers are written as:
2345= 2000+300+40+5
These when they have a bar over them can also be converted into normal numbers. For eg-:
2345= 2000+300-40+5 = 2265
Hence in the above example, the normal number for the above equation is 2265.
Another approach for the same is a process where we start from the right and go to the left. This is a trickier method by is very useful for numbers that have more digits.
Suppose we take the number 52113278235.
Now to convert this into a normal number, we will follow the below-given steps and move from right to left.
Find the 1st bar digit in the above-given number which in this case is 3 (from the right) and take its 10’s complement.
To find the “complement” of a number we subtract the given digit from the number. For eg: The 10’s complement for the number 7 is 3 (10-7)
A) If the next digit is a bar digit, take its 9’s complement. Continue until you reach a non-bar digit.
3. B) Decrement non-bar digit by 1.
4. Continue steps 1) and 2) until the whole number is covered.
Therefore, the normal number in the above case will come out to be 47913122175.
Now that we’ve gotten a quick recap of the Vinculum Process, we can now move on to learning this particular Sutra which is called Paryavarta Yojayeta.
Suppose we take 2 numbers:
587 and 11.
Make two columns and divide the dividend into two parts. Always remember that the 2nd part of the number should be a digit less than the divisor. In this case, the number will be divided into (1) 58 and (2) 7.
The divisor can be written as 11/1.
Now, as our sutra says we have to transpose and apply. Therefore, for the first step, we will pull the number 5 down as shown below.
Figure 1
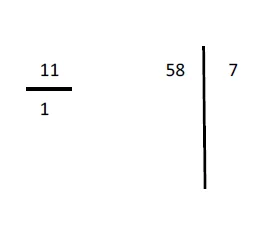
This 5 will be multiplied by 1(from the divisor 11/1) according to the sutra.
(5*1) will give us 5 which will be written below 8 from the dividend as shown below.
Figure 2
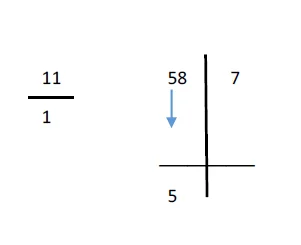
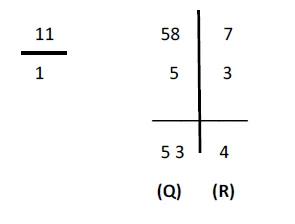
Now, as we perform the process in modern division methods, this 5 will be subtracted from 8 giving us 3.
3 will again be multiplied by 1 from the divisor and its answer will be subtracted from the remaining digit of the dividend i.e 7 which will be equal to 4.
Hence, we now have our quotient and remainder for the following equation.
Quotient = 53, Remainder = 4
Figure 3
Paryavarta Yojayet
Let’s try this with another example:
Suppose we take 2 numbers:
253 and 11.
Make two columns and divide the dividend into two parts. Always remember that the 2nd part of the number should be a digit less than the divisor. In this case, the number will be divided into (1) 25 and (2) 3.
The divisor can be written as 11/1.
Now, as our sutra says we have to transpose and apply. Therefore, for the first step, we will pull the number 2 down as shown below.
Figure 4
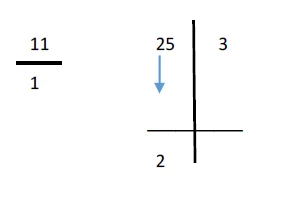
This 2 will be multiplied by 1(from the divisor 11/1) according to the sutra.
(2*1) will give us 2 which will be written below 5 from the dividend as shown below.
Now, as we perform the process in modern division methods, this 2 will be subtracted from 5 giving us 3.
3 will again be multiplied by 1 from the divisor and its answer will be subtracted from the remaining digit of the dividend i.e 3 which will be equal to 0.
Hence, we now have our quotient and remainder for the following equation.
Quotient = 23, Remainder = 0
Figure 5
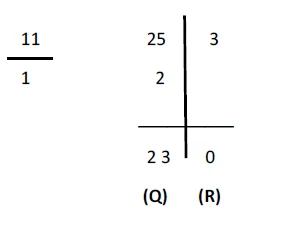
With this, we’ve learnt the trick for the division of 3 digit numbers. Fun and quick, isn’t it?
This method can also be applied for the division of numbers with a greater number of digits. We’ll now see how this works-
Vedic algebra:- Paryavarta Yojayet
Suppose we take two numbers;
28732 and 112, where 28732 is the dividend and 112 is the divisor
Divide the number into two parts. The 2nd part of the number is a digit lesser than the divisor. Therefore, the number is divided into (1) 287 and (2) 32.
For the divisor, the first digit is ignored and the other digits are transposed. Therefore from the number 112, the first 1 is ignored and the remaining 1 and 2 that are positive will be converted into negative digits ie. Bar 1 and Bar 2.
The divisor will now be written as 112/ 1 2
Let us start the division process. Bring down 2 and multiply it by Bar 1 and Bar 2. The answer will be Bar 2 and Bar 4(write it below 7) as shown here.
As the normal division process takes place, subtract the next equation i.e. 8 – Bar 2. The answer is 6.
Again, multiply 6 by Bar 1 and Bar 2. This will give you Bar 6 and Bar 12. Carry on the multiplication and subtraction procedure till you reach the last digits.
The first answer would come out to be 263 as quotient 68 as remainder.
Using the vinculum method our final answer can be written as 25660.
Figure 6
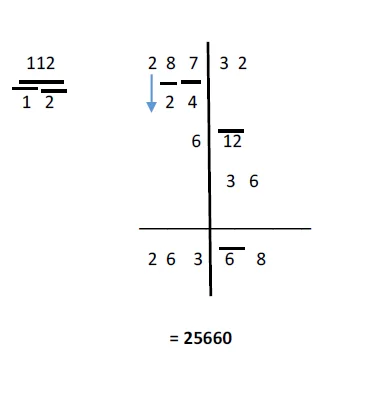
Hope you learned about Paryavarta Yojayet sutra. Keep practising till you become an expert in this. Paryavarta Yojayet is one of the many Sutras that’ll help you in the quick division.
2345= 2000+300-40+5 = 2265
For the divisor, the first digit is ignored and the other digits are transposed. Therefore from the number 112, the first 1 is ignored and the remaining 1 and 2 that are positive will be converted into negative digits ie. Bar 1 and Bar 2.
The first answer would come out to be 263 as quotient 68 as remainder.
